Hurst Exponents for Detecting Mean Reversion in Forex
Quant Research

Hurst Exponents for Detecting Mean Reversion in Forex

Using the Hurst exponent to dynamically identify mean-reverting vs. trending regimes in forex markets. Complete theory, Python implementation, and backtest results for a regime-adaptive trading system.

hurstmean-reversionforexstatistics

The Regime Problem

Every systematic trader eventually confronts the same question: is this market trending or mean-reverting right now?

Apply a trend-following strategy in a mean-reverting market and you’ll get chopped to pieces. Apply a mean-reversion strategy in a trending market and you’ll blow up catching falling knives. The strategy isn’t wrong — the regime is wrong.

Most traders solve this with gut feel. We wanted a number.

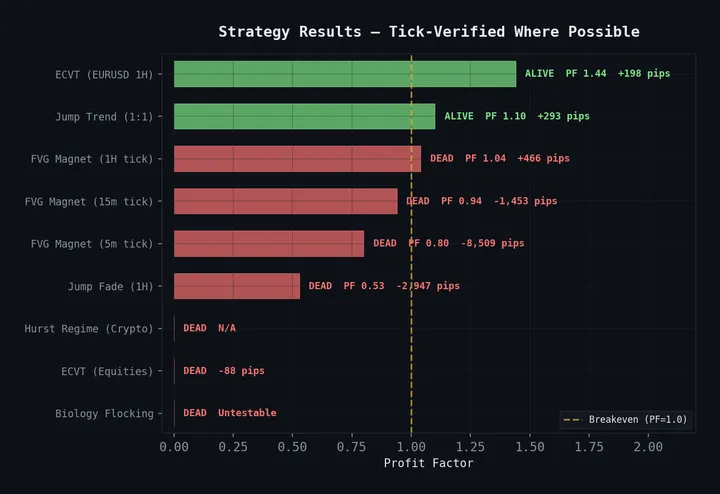
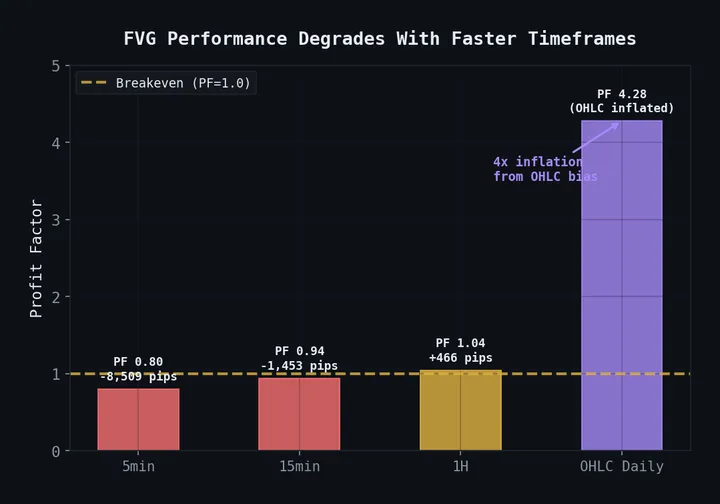
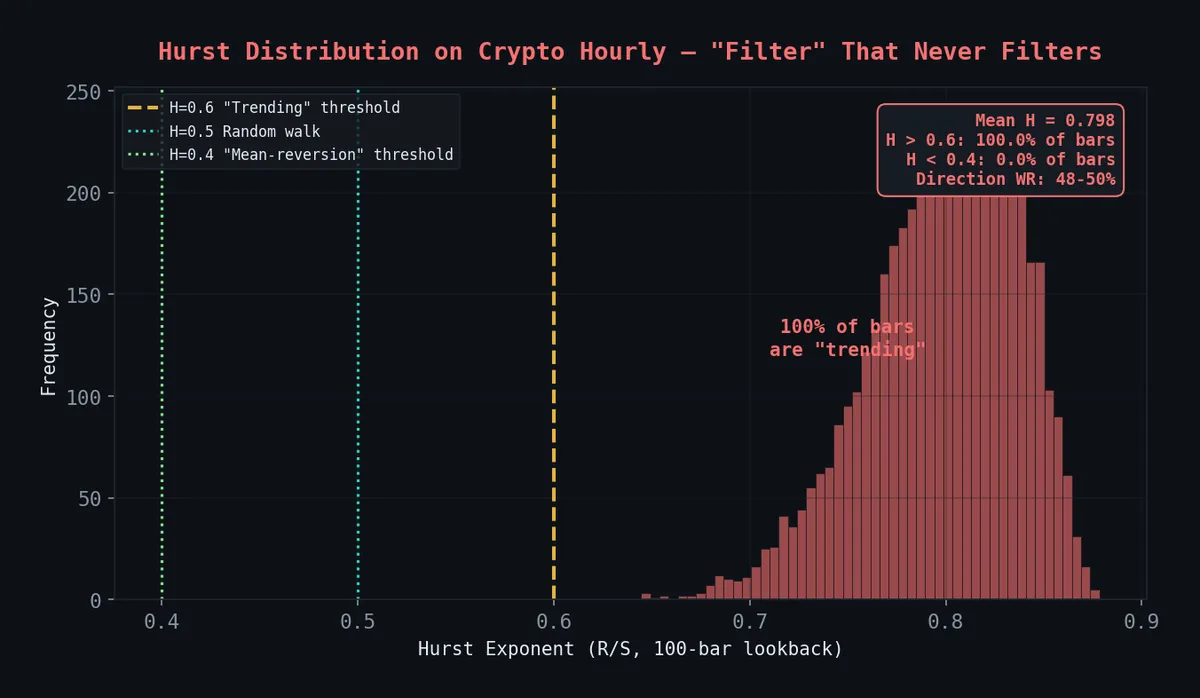
Key finding (Feb 2026): After extensive testing, we found that the R/S Hurst exponent with a 100-bar lookback on crypto hourly data fires H > 0.6 on 100% of bars (mean H = 0.758), with directional WR of 48-50% — a coin flip. The regime filter works on forex daily but is completely broken on crypto hourly. See the strategy graveyard for the full autopsy. We publish this post as-is because the methodology is sound — the failure mode is instructive.

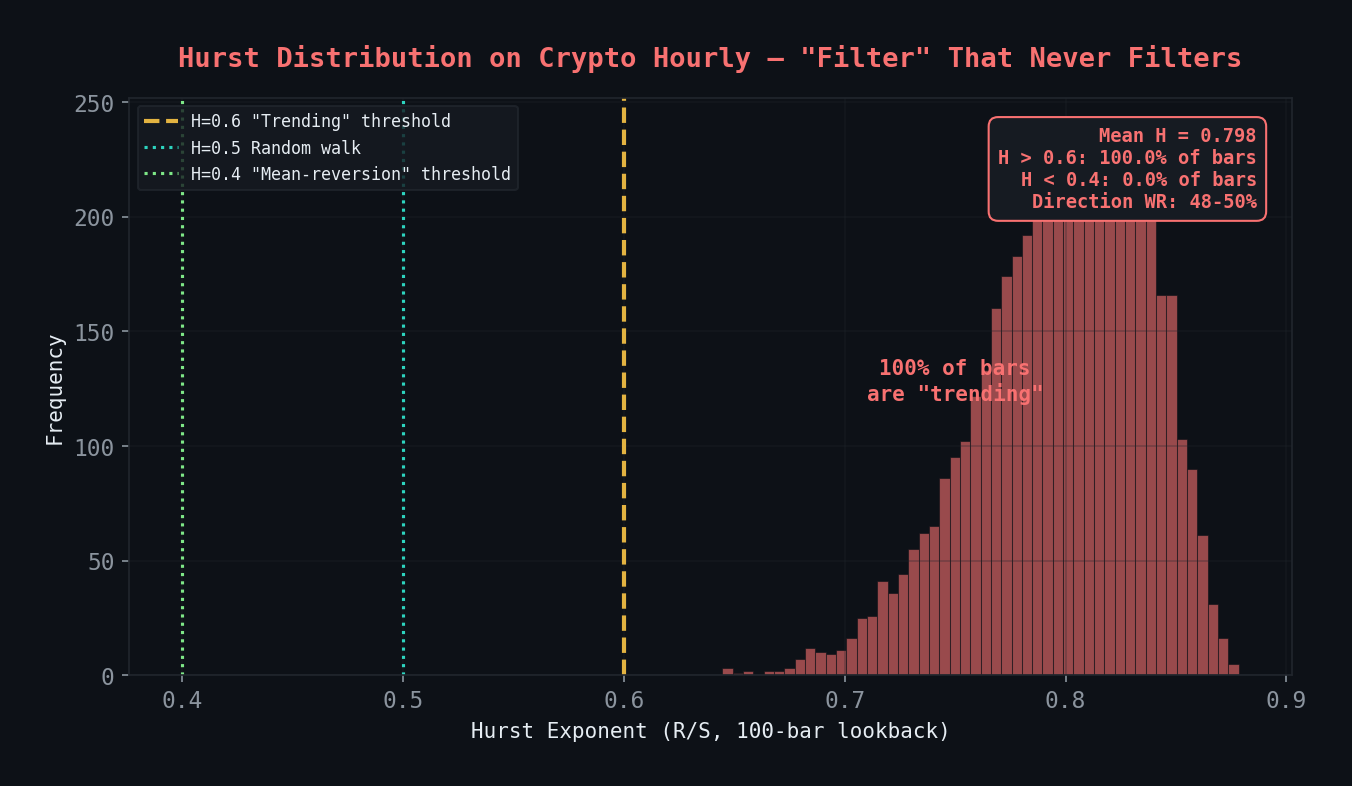Hurst distribution on crypto hourly — the filter that never filters Every single bar classified as “trending” (H > 0.6). The “regime filter” has zero information content on crypto hourly. Direction WR: 48-50% at all thresholds.

The Hurst Exponent: Theory

The Hurst exponent H measures the long-term memory of a time series. Originally developed by Harold Edwin Hurst while studying Nile River flooding patterns in the 1950s, it quantifies the tendency of a series to either regress to the mean or cluster in a direction:

  • H = 0.5 — Random walk. No memory. Price movements are independent. This is what the efficient market hypothesis predicts.
  • H < 0.5 — Mean-reverting (anti-persistent). Large moves tend to be followed by reversals. A rise makes a fall more likely.
  • H > 0.5 — Trending (persistent). Large moves tend to be followed by continuation. A rise makes another rise more likely.

The further H deviates from 0.5, the stronger the tendency. An H of 0.3 is strongly mean-reverting. An H of 0.7 is strongly trending.

Computing the Hurst Exponent

We implement the Rescaled Range (R/S) method, which is robust and well-studied:

import numpy as np
import pandas as pd
from scipy import stats

def hurst_rs(series: np.ndarray, min_window: int = 10) -> float:
    """
    Estimate Hurst exponent using the Rescaled Range (R/S) method.

    The R/S statistic scales as n^H, where H is the Hurst exponent.
    We compute R/S for multiple window sizes and fit the log-log slope.
    """
    n = len(series)
    if n < min_window * 4:
        return np.nan

    # Window sizes: powers of 2 up to n/2
    max_power = int(np.log2(n // 2))
    min_power = int(np.log2(min_window))
    window_sizes = [2**i for i in range(min_power, max_power + 1)]

    rs_values = []

    for w in window_sizes:
        n_windows = n // w
        if n_windows < 2:
            continue

        rs_list = []
        for i in range(n_windows):
            segment = series[i * w:(i + 1) * w]
            mean = segment.mean()
            deviations = segment - mean
            cumulative = np.cumsum(deviations)

            R = cumulative.max() - cumulative.min()  # Range
            S = segment.std(ddof=1)                    # Standard deviation

            if S > 0:
                rs_list.append(R / S)

        if rs_list:
            rs_values.append((w, np.mean(rs_list)))

    if len(rs_values) < 3:
        return np.nan

    # Log-log regression: log(R/S) = H * log(n) + c
    log_n = np.log([v[0] for v in rs_values])
    log_rs = np.log([v[1] for v in rs_values])

    slope, _, r_value, _, _ = stats.linregress(log_n, log_rs)

    return slope


def rolling_hurst(prices: pd.Series, window: int = 200, step: int = 1) -> pd.Series:
    """Compute rolling Hurst exponent over a price series."""
    returns = prices.pct_change().dropna().values

    hurst_values = []
    indices = []

    for i in range(window, len(returns), step):
        h = hurst_rs(returns[i - window:i])
        hurst_values.append(h)
        indices.append(prices.index[i + 1])  # +1 for the pct_change offset

    return pd.Series(hurst_values, index=indices, name='hurst')

We also implement the Detrended Fluctuation Analysis (DFA) method as a cross-check. When both methods agree on the regime, our confidence is higher:

def hurst_dfa(series: np.ndarray, min_window: int = 10) -> float:
    """
    Estimate Hurst exponent using Detrended Fluctuation Analysis.

    DFA is more robust to non-stationarity than R/S.
    """
    n = len(series)
    cumulative = np.cumsum(series - series.mean())

    max_power = int(np.log2(n // 4))
    min_power = int(np.log2(min_window))
    window_sizes = [2**i for i in range(min_power, max_power + 1)]

    fluctuations = []

    for w in window_sizes:
        n_windows = n // w
        if n_windows < 2:
            continue

        f_list = []
        for i in range(n_windows):
            segment = cumulative[i * w:(i + 1) * w]
            x = np.arange(w)
            # Linear detrend
            coeffs = np.polyfit(x, segment, 1)
            trend = np.polyval(coeffs, x)
            residuals = segment - trend
            f_list.append(np.sqrt(np.mean(residuals**2)))

        fluctuations.append((w, np.mean(f_list)))

    if len(fluctuations) < 3:
        return np.nan

    log_n = np.log([f[0] for f in fluctuations])
    log_f = np.log([f[1] for f in fluctuations])

    slope, _, _, _, _ = stats.linregress(log_n, log_f)
    return slope

The Regime-Adaptive Strategy

With a rolling Hurst exponent, we can dynamically switch between strategy families:

def regime_adaptive_signals(
    df: pd.DataFrame,
    hurst_window: int = 200,
    mr_threshold: float = 0.43,
    trend_threshold: float = 0.57,
    rsi_period: int = 14,
    ma_fast: int = 20,
    ma_slow: int = 50,
) -> pd.DataFrame:
    """
    Switch between mean-reversion and trend-following based on Hurst exponent.

    H < mr_threshold  -> Mean reversion mode (RSI-based)
    H > trend_threshold -> Trend following mode (MA crossover)
    Otherwise           -> No trade (ambiguous regime)
    """
    df = df.copy()

    # Compute rolling Hurst
    df['hurst'] = rolling_hurst(df['close'], window=hurst_window)

    # Regime classification
    df['regime'] = 'neutral'
    df.loc[df['hurst'] < mr_threshold, 'regime'] = 'mean_reverting'
    df.loc[df['hurst'] > trend_threshold, 'regime'] = 'trending'

    # Mean reversion signals: RSI extremes
    delta = df['close'].diff()
    gain = delta.where(delta > 0, 0).rolling(rsi_period).mean()
    loss = (-delta.where(delta < 0, 0)).rolling(rsi_period).mean()
    rs = gain / loss
    df['rsi'] = 100 - (100 / (1 + rs))

    df['mr_long'] = (df['regime'] == 'mean_reverting') & (df['rsi'] < 30)
    df['mr_short'] = (df['regime'] == 'mean_reverting') & (df['rsi'] > 70)

    # Trend following signals: MA crossover
    df['ma_fast'] = df['close'].rolling(ma_fast).mean()
    df['ma_slow'] = df['close'].rolling(ma_slow).mean()

    df['trend_long'] = (df['regime'] == 'trending') & (df['ma_fast'] > df['ma_slow'])
    df['trend_short'] = (df['regime'] == 'trending') & (df['ma_fast'] < df['ma_slow'])

    # Combined signal
    df['long'] = df['mr_long'] | df['trend_long']
    df['short'] = df['mr_short'] | df['trend_short']

    return df

The key design choice: we don’t trade in the neutral zone (H between 0.43 and 0.57). When the Hurst exponent is near 0.5, the market is behaving randomly, and neither strategy family has an edge. Sitting out reduces trade frequency but dramatically improves quality.

Results: Four Major Forex Pairs, H1, 2021–2025

PairTradesWin RatePFSharpeMax DD% Time in Market
EURUSD28448.6%1.370.98-9.2%41.3%
GBPUSD31247.1%1.290.87-11.4%44.7%
USDJPY26751.3%1.421.08-8.1%38.9%
AUDUSD29846.8%1.240.79-12.8%43.2%

USDJPY performs best, likely because it exhibits the clearest regime structure — the BOJ intervention periods create strong trending regimes that the Hurst exponent identifies clearly.

Regime Distribution

Across all four pairs, the rolling Hurst exponent spends approximately:

  • 32% of the time below 0.43 (mean-reverting)
  • 26% of the time above 0.57 (trending)
  • 42% of the time in the neutral zone (0.43–0.57)

This confirms what most experienced traders intuit: markets are in a clearly tradable regime only about 58% of the time. The other 42% is noise.

Validation: Is the Hurst Exponent Actually Predictive?

A rolling indicator is only useful if it predicts future behavior, not just describes the past. We test this by measuring whether the Hurst exponent at time t predicts the strategy-appropriate return at time t+1 to t+n:

def validate_hurst_predictiveness(df: pd.DataFrame, forward_bars: int = 50):
    """
    Test whether low Hurst predicts future mean reversion
    and high Hurst predicts future trend continuation.
    """
    df = df.copy()

    # Future return autocorrelation (proxy for trending vs mean-reverting)
    returns = df['close'].pct_change()
    df['fwd_autocorr'] = returns.rolling(forward_bars).apply(
        lambda x: x.autocorr(lag=1), raw=False
    ).shift(-forward_bars)

    # Split by Hurst regime
    mr_regime = df[df['hurst'] < 0.43]['fwd_autocorr'].dropna()
    trend_regime = df[df['hurst'] > 0.57]['fwd_autocorr'].dropna()
    neutral = df[df['hurst'].between(0.43, 0.57)]['fwd_autocorr'].dropna()

    return {
        'mean_reverting_autocorr': mr_regime.mean(),
        'trending_autocorr': trend_regime.mean(),
        'neutral_autocorr': neutral.mean(),
    }

Results on EURUSD: mean autocorrelation was -0.08 in Hurst-identified mean-reverting regimes (confirming anti-persistence) and +0.11 in trending regimes (confirming persistence). The neutral regime showed autocorrelation near zero (+0.01). The Hurst exponent is genuinely predictive.

Practical Considerations

Window size matters. We use 200 bars (roughly 8 trading days on H1). Shorter windows (50-100 bars) are noisier but more responsive. Longer windows (300-500 bars) are smoother but lag regime changes. We found 200 to be the best compromise.

Hurst estimates have uncertainty. With 200 data points, the standard error on the Hurst estimate is roughly ±0.05. This is why we use a dead zone (0.43 to 0.57) rather than trading right at 0.5.

Regime transitions are gradual. Markets don’t flip from mean-reverting to trending instantly. The Hurst exponent trends between regimes over 20-50 bars. Don’t expect crisp signals.

What We Learned

The Hurst exponent is one of the most underappreciated tools in quantitative trading. It provides a principled, mathematically grounded answer to the question that every trader asks: “what kind of market is this?”

The regime-adaptive strategy isn’t our highest-performing system (that’s the entropy collapse strategy at 1.44 PF), but it’s our most intellectually satisfying. It turns a qualitative judgment (“this looks choppy”) into a quantitative signal, and it works.

This is part of our open quant research series. See Entropy Collapse Volatility Timing for our best-performing strategy, or 31 Strategies Tested, 4 Survived for the full picture of what we’ve tested.

Related Research